*Wikipedia 내용을 해석한 것이며 개인적인 관련지식 습득을 위해 작성된 자료로 학계에서 통용되어 쓰지 않는 한글 해석 용어가 포함되어 있을 수 있음.
Ref:
http://en.wikipedia.org/wiki/Quasiperiodic_function
http://en.wikipedia.org/wiki/Weierstrass%27s_elliptic_functions
http://en.wikipedia.org/wiki/Elliptic_function
수학에서 주기함수(periodic function) 함수와 유사하나 엄격하게 그 정의를 만족하지 못하는 함수를 Quasiperiodic(준주기적) 이라 한다.
f(z+ω) = g(z,f(z)), 이때 g는 f보다 "더 간단한 (simpler)" 함수이다 - simpler의 의미는 사실상 모호하게 사용된다.
이때, 함수 f는 준주기 ω를 가지는 Quasiperiodic 이다.
함수가 다음의 방정식을 따른다면 산술적 준주기(Arithmetic quasiperiodic)의 간단한 예이다.
f(z+ω) =f(z) + C
또 다른 하기의 방정식은 기하학적 준주기(Geometric quasiperiodic)의 간단한 예이다.
f(z+ω) = Cf(z)
유용하게 사용될 수 있는 함수는 다음의 식이다.
f(z) = sin(Az) + sin(Bz)
- 비율 A/B가 유리수(rational)라면 상기 함수는 정확한 주기(true period)를 가진다.
- 비율 A/B가 무리수(irrational)라면 상기 함수는 정확한 주기가 없다. (그러나 주기가 점점 정확해지는 하나의 연속임)
또 하나의 준주기함수의 예는 Jacobi theta 함수이며 다음과 같다.

이식은 고정된 τ 에 대해서 보여주는데, 이때 τ는 준주기(quasiperiod)이며, 이 함수는 또한 주기 하나를 가지는 주기함수이다.
다른 예는 Weierstrass sigmal function이다. 이 함수는 두개의 독립적인 준주기(quasiperiod)를 가지는 준주기적 함수이다.
이때 주기들은 Weierstrass ℘ function 에 해당한다.
부가적인 함수가 들어간 방정식의 예는 다음과 같다.
f(z+w) = f(z) + az + b
이 또한 준주기적이다라고 하는데 이 것의 예로 Weierstrass zeta function이 있다.

이는 w가 Weierstrass ℘ function에 해당하는 주기일때 고정된 η에 대한 함수이다.
특별한 케이스로
f(z+w) = f(z) 가 있는데 이 때 f는 주기적이고 이 때 주기는 w라고 한다.
*Weierstrass's elliptic functions
-일종의 타원형 함수(Elliptic functions)
>두개의 방향으로 주기적인 Meromorphic fuctions (유리형,有理型)
>보통의 실수형 주기함수는 하나의 주기에 의해 결정되는데 타원형 함수는 기본적인 평행4변
(fundamentalparallelogram)상의 값들에 의해 결정된다 (하나의 격자 안에서 반복됨)
>이러한 이중 주기함수(doubly periodic function)는 해석(解析)적(holomorphic)일 수 없다.
따라서 경계 전체 함수(bounded entire function)가 될 수 있고 Liouville's theorem에 의해 모든 개별 함수는
불변(constant)이다.
>실질적으로 타원형 함수는 최소 2개의 pole들을 (counting multiplicity) 기본적인 평행4변형 내에 가져야함
>Periodicity(주기성)를 사용하면 반드시 소멸되어야하는 경계선 주위의 contour integral (폐곡선 적분), 간단
pole들의 잔차들이 반드시 무효화 되어야 함을 의미한다는 것에 대해 쉽게 설명이 가능하다.
-이러한 함수들의 클래스를 P-functions로 부르기도 하며 일반적으로 ℘ ("Weierstrass P")를 사용하여 표시함
-Weisserstrass 타원함수는 3가지 연관된 방식으로 정의가 가능하다.
1) 복소평면(가우스 평면) 안에서 복소변수 z와 lattice(격자) Λ 의 함수
2) Lattice(격자에 대해) 복소변수 z와 Generators(또는 주기) 쌍으로 정의되는 두개의 복소수 ω1과 ω2로 구성되
는 함수
3) Upper half-plane(상반평면) 상에서 복소변수 z와 modulus τ 로 구성되는 함수 ( τ = ω2/ω1 : 이것은 상반평
면 내에서 주기들의 쌍을 선택하는 전통적인 방법에 의함), 이 방법의 사용하면, 고정된 z에 대해 Weierstrass
function들은 τ 의modular function이 된다.
- 두 주기에 대해 Weierstrass's elliptic function은 주기 ω1과 ω2의 타원형 함수이며 다음과 같이 정의됨
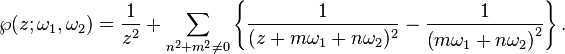
그렇다면,  는 Period lattice (주기 격자)의 포인트들이다.
는 Period lattice (주기 격자)의 포인트들이다.
따라서, 
상기의 함수는 격자의 어떠한 Generator들의 쌍에 대해 하나의 복소변수와 하나의 lattice의 함수로 Weierstrass
function을 정의한다.
만약, τ 가 상반평면 내에서 하나의 복소수라면,

상기의 합은 Degres minus 2의 homogeneous 이다. 이로부터 우리는 어떤 주기의 쌍에 대해서라도
Weierstrass ℘ 함수를 정의할 수 있다.

theta functions들의 측면에서 ℘를 매우 빠르게 계산할 수 있다. 왜냐하면 이들의 converge(수렴)은 매우 빠르고,
우리가 정의 한 것의 시리즈들 보다 ℘를 계산하는 보다 빠른 방법이다. 이에 대한 공식은 다음과 같다.
![\wp(z; \tau) = \pi^2 \vartheta^2(0;\tau) \vartheta_{10}^2(0;\tau){\vartheta_{01}^2(z;\tau) \over \vartheta_{11}^2(z;\tau)}-{\pi^2 \over {3}}\left[\vartheta^4(0;\tau) + \vartheta_{10}^4(0;\tau)\right]](http://upload.wikimedia.org/math/4/e/2/4e21b89d0e9918d8f063825e99633a5a.png)
- 주기격자(period lattice - including the origin)의 개별 포인트에 2차 pole들 이 있다. 이러한 정의들과 함께,
℘(z)는 even function이며 그것의 z, ℘' 에 관한 미분계수(도함수)는 odd function이 된다.
Weierstrass P function defined over a subset of the complex plane using a standard visualization technique in which white corresponds to a pole, black to a zero, and maximalsaturation to 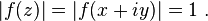 Note the regular lattice of poles, and two interleaving lattices of zeros. (wikipedia)
Note the regular lattice of poles, and two interleaving lattices of zeros. (wikipedia)
'Lab Notes' 카테고리의 다른 글
| R을 이용한 상관관계 분석 (0) | 2015.04.24 |
|---|---|
| Stationary process, Cyclostationary process (0) | 2014.12.17 |
| WEKA OutOfMemory 창이 뜰때 (0) | 2014.10.02 |
| WEKA 결과 화면 분석 (0) | 2014.10.01 |
| 파이썬 배포 패키지 생성 시 유의~ (0) | 2014.09.24 |


